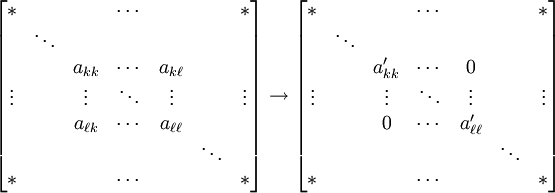
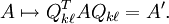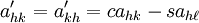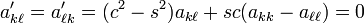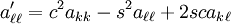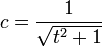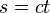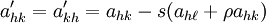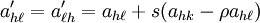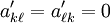雅克比旋转-白红宇

强烈建议你试试无所不能的chatGPT，快点击我

雅克比旋转

阅读量：5322 次

发布时间：2019-06-14

本文共 728 字，大约阅读时间需要 2 分钟。

在中，雅可比旋转是n 维的二维线性子空间的Q_kℓ，在用做的时候，被选择来置零n×n A 的非元素的对称对:

$A \mapsto Q_{k\ell}^T A Q_{k\ell} = A' . \,\!$

$\begin{bmatrix} {*} & & & \cdots & & & * \\ & \ddots & & & & & \\ & & a_{kk} & \cdots & a_{k\ell} & & \\ \vdots & & \vdots & \ddots & \vdots & & \vdots \\ & & a_{\ell k} & \cdots & a_{\ell\ell} & & \\ & & & & & \ddots & \\ {*} & & & \cdots & & & *\end{bmatrix}\to\begin{bmatrix} {*} & & & \cdots & & & * \\ & \ddots & & & & & \\ & & a'_{kk} & \cdots & 0 & & \\ \vdots & & \vdots & \ddots & \vdots & & \vdots \\ & & 0 & \cdots & a'_{\ell\ell} & & \\ & & & & & \ddots & \\ {*} & & & \cdots & & & *\end{bmatrix}$

它是的核心运算，它是的并适合用实现。

注意到只有 A 的行 k 和 ℓ 与列 k 和 ℓ 受到影响，并且 A′ 将保持对称。还有给Q_kℓ 的明显的矩阵很少被计算，转而计算辅助值，A 也有效率和数值上稳定的方式更新。但是，为了引用，我们写矩阵为

$Q_{k\ell} = \begin{bmatrix} 1 & & & & & & \\ & \ddots & & & & 0 & \\ & & c & \cdots & s & & \\ & & \vdots & \ddots & \vdots & & \\ & & -s & \cdots & c & & \\ & 0 & & & & \ddots & \\ & & & & & & 1\end{bmatrix} .$

就是说，除了四个元素之外，Q_kℓ 是一个单位矩阵，两个在对角线上(q_kk 和q_ℓℓ 都等于 c) 而两个位于远离对角的位置上(q_kℓ 和Q_ℓk 分别等于 s 和 −s)。这里的 c = cos ϑ 而s = sin ϑ 对于某个角度 ϑ；但是对于应用这种旋转，这个角度自身是不需要的。使用符号，矩阵元素可以写为

$q_{ij} = \delta_{ij} + (\delta_{ik}\delta_{jk} + \delta_{i\ell}\delta_{j\ell})(c-1) + (\delta_{ik}\delta_{j\ell} - \delta_{i\ell}\delta_{jk})s . \,\!$

假设 h 是不为 k 或 ℓ 的索引(它们自身必须是不同的)。类似的更改过程在代数上写为

$a'_{hk} = a'_{kh} = c a_{hk} - s a_{h\ell} \,\!$

$a'_{h\ell} = a'_{\ell h} = c a_{h\ell} + s a_{hk} \,\!$

$a'_{k\ell} = a'_{\ell k} = (c^2-s^2)a_{k\ell} + sc (a_{kk} - a_{\ell\ell}) = 0 \,\!$

$a'_{kk} = c^2 a_{kk} - s^2 a_{\ell\ell} - 2 s c a_{k\ell} \,\!$

$a'_{\ell\ell} = c^2 a_{kk} - s^2 a_{\ell\ell} + 2 s c a_{k\ell} \,\!$

数值稳定计算

要确定需要更改的数量，我们必须解远离对角的元素为零的方程（，§8.4）

。这蕴涵了

$\frac{c^2-s^2}{sc} = \frac{a_{\ell\ell} - a_{kk}}{a_{k\ell}} .$

设 β 是这个数量的一半，

$\beta = \frac{a_{\ell\ell} - a_{kk}}{2 a_{k\ell}} .$

如果 a_kℓ 是零，我们可以停止而不需要进行更改，因此我们永不除以零。设 t 是 tan ϑ。则通过一些三角恒等式我们简约这个方程为

$t^2 + 2\beta t - 1 = 0 . \,\!$

为了稳定性我们选择解

$t = \frac{\sgn(\beta)}{|\beta|+\sqrt{\beta^2+1}} .$

以此我们可以获得 c 和 s 为

$c = \frac{1}{\sqrt{t^2+1}} \,\!$

$s = c t \,\!$

尽管我们可以使用前面给出的代数更改等式，重写它们会更好。设

$\rho= \frac{s}{1+c} ,$

所以 ρ = tan(ϑ/2)。则修订后的修改方程为

$a'_{hk} = a'_{kh} = a_{hk} - s (a_{h\ell} + \rho a_{hk}) \,\!$

$a'_{h\ell} = a'_{\ell h} = a_{h\ell} + s (a_{hk} - \rho a_{h\ell}) \,\!$

$a'_{k\ell} = a'_{\ell k} = 0 \,\!$

$a'_{kk} = a_{kk} - t a_{k \ell} \,\!$

$a'_{\ell\ell} = a_{\ell\ell} + t a_{k \ell} \,\!$

如前面提及的，我们永不需要明确的计算旋转角度 ϑ。事实上，我们可以通过只保留三个值 k, ℓ 和 t 来重新生成由 Q_kℓ 确定的对称更改，带有 t 对零旋转设置为零。

转载于:https://www.cnblogs.com/cl1024cl/p/6205227.html

你可能感兴趣的文章

poj2388---求奇数个数字的最中间的数

对闭包的理解

java.lang.OutOfMemoryError异常解决方法

Css让文字自适应Table宽度[转]

[Javascript] Flattening nested arrays: a little exercise in functional refactoring

练习10-1 使用递归函数计算1到n之和（10 分

使用maven构建多模块项目，分块开发

Oracle MySQL yaSSL 不明细节缓冲区溢出漏洞2

windows编程ASCII问题

.net webService代理类

C#高级编程笔记（一）

MFC模态对话框程序不响应OnIdle

Node.js Express项目搭建

zoj 1232 Adventure of Super Mario

Oracle 序列的应用

1201 网页基础--JavaScript(DOM)

组合数学 UVa 11538 Chess Queen

Redis常用命令

喝酒易醉，品茶养心，人生如梦，品茶悟道，何以解忧？唯有杜康！-- 愿君每日到此一游！

当前时间: 2024-11-28 05:39:21 当前IP: 18.191.103.144 联系邮箱:javaeecc@qq.com Copyright © 2020 - 2022 baihongyu.com 京ICP备2021015314号-2

强烈建议你试试无所不能的CHAT-GPT，快点击我

强烈建议你试试无所不能的CHAT-GPT，快点击我